深度学习如何提升手工量价因子表现

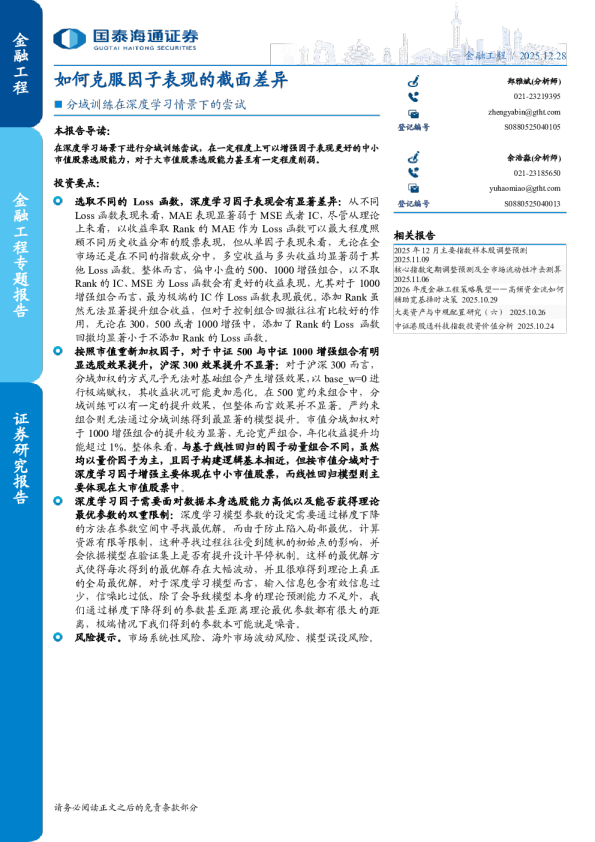
请务必阅读正文之后的免责条款部分深度学习如何提升手工量价因子表现利用深度学习解释现有手工选股因子残差方案与实践本报告导读：除开直接使用深度学习模型得到股票预期收益之外，通过将需要使用的收益因子加入正交层当中，可以得到与现有收益因子低相关，但依然具有良好选股效果的深度学习因子。从而在后续使用中，方便对于因子权重的人工调整。投资要点：[Table_Summary]将收益因子加入正交层，可以使得同源深度因子在保证选股效果前提下，与正交层收益因子低相关：深度学习模型有黑盒化的特征，当市场出现剧烈风格转换时，很难通过人工的方法对于模型进行干预，手工改变不同因子的权重。而通过将收益因子加入深度学习模型正交层，可以在保障深度因子选股效果的同时，降低深度因子与正交层中收益因子相关性，防止在构建手工多因子组合时，深度因子与同源其他手工收益因子的多重共线性问题。在正交层放入其他同源收益因子后，深度因子依然有非常良好的选股效果：无论是以Rank MAE还是IC为Loss函数，将以高频量价，低频量价手工构建的收益因子放入正交层后，深度因子依然具有0.02以上的IC以及6以上的IC IR，其在全市场中依然有一定的选股效果。将深度因子与手工收益因子放在一起构建多因子组合时，与不放入深度因子相比，其全市场多头组合有明显的改善，但在不同指数增强组合中提升效果会有所波动。正交层放入收益因子后，深度因子与多粒度因子相关性依然较低，共同构建全市场多头组合相比较单独使用多粒度因子有更好的表现：正交层放入收益因子后，深度因子与多粒度因子依然有较低的相关性，高频数据作为输入的深度因子与多粒度因子相关性不超过0.01，将深度因子与多粒度因子共同使用可以明显提全市场纯多头组合的表现，但受限于深度学习因子对于偏中、大市值股票收益预测能力的不足，对于指数增强组合改善效果并不明显。风险提示。市场系统性风险、海外市场波动风险、模型误设风险。 目录1.深度学习模型在因子构建中的应用..............................................................32.解释手工因子残差的深度因子构建与市场表现...........................................32.1.深度因子的单因子表现............................................................................42.2.深度因子在组合中的表现........................................................................53.解释手工因子残差的深度因子对于多粒度因子的提升...............................83.1.正交多粒度因子后的解释手工因子残差的深度因子表现....................83.2.深度因子与多粒度因子复合因子组合表现............................................94.总结................................................................................................................125.风险提示........................................................................................................12 请务必阅读正文之后的免责条款部分2of13 请务必阅读正文之后的免责条款部分3of131.深度学习模型在因子构建中的应用目前，深度学习模型已经广泛的应用到多因子选股过程当中，而其中最为常规的做法是将所有参与选股的手工因子作为深度模型输入，通过深度学习直接获得预期收益向量，并以该预期收益向量构建多因子组合。显然，从挖掘数据选股信息角度来说，这种方式可以最大限度的利用深度模型的拟合能力，提取出手工因子的有效选股信息。然而，由于深度模型具有黑盒的特性，我们无法对于输入的手工因子进行人为的权重调整。深度学习模型得到的因子权重完全由历史数据学习得到，当市场风格出现历史数据中没有出现的变动时，或者我们需要对于组合风格进行人为控制时，这样的组合构建方式很难让我们达到预期的权重调整效果。为了最大限度利用深度学习模型的拟合能力，同时保留我们对于不同输入手工因子的权重手工调整可能性，我们尝试一种新的深度学习因子构建方式，即：在模型输出层前，加入复杂的正交层，其中包含我们构建组合时需要使用的手工选股因子。通过正交层，使得深度因子与我们需要使用的手工选股因子线性无关。因子使用时，将添加正交层的深度因子与手工因子一起利用传统的线性方法，如因子动量计算股票预期收益，从而构建因子组合。这样的构建方法，本质上相当于利用深度学习模型强大的拟合能力，为我们在手工因子无法解释的残差部分，进一步提取有效选股信息，其与传统方式差别如下图：图2：解释手工因子残差的深度因子模型数据来源：国泰海通证券研究2.解释手工因子残差的深度因子构建与市场表现基于上述深度学习因子构建方法调整，我们尝试构建了解释手工低频量价因子残差的深度因子，以及解释手工高频因子残差的深度因子两类因子。其中，低频深度因子的构建方式如下：输入数据：日度高开低收收益率，日度换手，日度反转，日度非流动性，日度特质波动动，日度市值，日度非线性市值，日度PB等深度模型：LSTM数据长度：1个季度正交层因子：市值，非线性市值，估值，换手率，特质波动，反转，非流动性。Loss函数：IC、Rank MAE（只对收益率取Rank）训练周期：季度训练数据：13个季度（训练集12个季度，测试集1个季度）其中，高频深度因子的构建方式如下：输入数据：30分钟高频偏度，30分钟下行波动占比，30分钟买入意愿，30分钟买入意愿强度，30分钟大|中|小单净买入占比，30分钟大|中|小单净买入强度，30分钟成交占比，30分钟平均单笔流出金额，30分钟大单推动涨幅等深度模型：LSTM深度学习因子|预期收益计算预期收益手工因子正交后的深度因子手工高频量价手工日频量价基本面数据带正交的深度因子训练 多因子模型股票预期收益 数据来源：国泰海通证券研究 数据长度：20个交易日*830分钟正交层因子：市值，非线性市值，估值，换手率，特质波动，反转，非流动性，大单净买入占比，尾盘成交占比，买入意愿强度。Loss函数：IC、Rank MAE（只对收益率取Rank）训练周期：周度训练用数据：过去24个周（训练集20个周，测试集1个周）2.1.深度因子的单因子表现我们考察深度的单因子表现，如下表：表1深度因子单因子表现（2017.01-2025.04）RankMAERankMAE波动多头收益多头胜率多空收益多空胜率1.1300.0570.08%48.4%0.18%56.6%1.1280.0440.15%55.6%0.40%64.3%1.1470.0380.07%51.2%0.10%55.4%1.0860.0530.18%60.8%1.11%71.4%1.1200.0300.27%68.5%0.80%80.8%1.1310.0160.28%72.6%0.82%87.3%1.1340.0160.21%70.8%0.46%78.8%1.1260.0200.23%66.1%0.85%84.9%1.1250.0190.18%66.1%0.59%80.0%其中，基本面复合因子为过去52周ROE与SUE的线性回归复合因子，日频手工量价为换手，特质波动，反转，非流动性等手工日频量价因子的线性回归复合因子，高频手工量价则为高频偏度，下行波动占比，开盘买入意愿强度，开盘买入意愿占比，开盘大单净买入强度，开盘大单净买入占比，改进反转，尾盘成交占比，大单推动涨幅，平均单笔流出金额占比等手工高频量价因子的线性回归复合因子。从中我们也可以看出，本文的日频深度因子正交层加入了前述除高频外的所有因子，高频深度因子正交层加入了前述包括高频因子在内的所有因子，因此深度因子可以认为在对于前述手工因子无法解释的收益残差部分进行解释，挖掘增量信息。从上表单因子表现来看，无论是高频深度因子，还是日频深度因子，在正交掉市值、估值、行业等风格因子后，依然有非常高的IC表现，ICIR非常高，说明深度因子IC非常稳定。尤其日频深度因子，多头端相较于日频手工量价因子有明显提升，说明深度学习模型挖掘了残差中更多的多头选股信息。比较以IC和Rank MAE为Loss函数的不同深度因子，显然以RankMAE为Loss函数会明显牺牲因子的IC与多空表现，而如果比较因子RankMAE均值，以Rank MAE为Loss函数的深度因子依然略高于以IC为Loss函数的深度因子，但其指标差异远小于IC的差异。以Rank MAE为Loss函数会牺牲掉因子的多空选股效果，从而尽可能保证中间分组的收益预测能力。然而这种妥协并不一定导致Rank MAE为Loss函数的因子一定具有更小的Rank MAE表现。深度学习因子学习过程中往往有早停机制防止过拟合与计算资源浪费，训练迭代次数也不可能是无限的，因此如果输入数据包含的对于不同分组收益预测收益预测的信息有限，则实际训练中Rank MAE为Loss函数很有可能相较于IC为Loss函数更容易终止训练，训练模型更容易欠拟合或者对于测试集预测能力较低，进而导致牺牲IC为代价并没有迎来Rank MAE指标的改善。 请务必阅读正文之后的免责条款部分4of13 请务必阅读正文之后的免责条款部分5of13数据来源：Wind，国泰海通证券研究表2深度因子与常用风险因子，收益因子相关性（2017.01-2025.04）市值市值平方高频深度（IC）-0.0010.010高频深度（MAE）0.0000.013日频深度（IC）-0.0020.010日频深度（MAE）-0.0040.011资料来源：Wind，国泰海通证券研究所 数据来源：Wind，国泰海通证券研究从分组收益来看，以Rank MAE为Loss函数明显牺牲了多空收益，同时分组单调性也没有得到本质性改善。因此，单单从单因子指标来看，并没有达到预期的提升中间分组收益预测能力的效果。最后我们考察深度因子与其他因子相关性情况，如下表：基本面复合分红日频手工量价0.0160.001-0.0030.0130.0030.0000.0470.008-0.0070.0400.021-0.005从相关系数角度来看，无论与风险因子还是常用的收益因子，相关性都非常低，最高相关性不到0.05。这说明复杂正交层的确起到了剥离深度因子与其他因子之间相关性的效果，而在剥离相关性后，深度因子依然保留较好2.2.深度因子在组合中的表现我们将高频深度因子与日频深度因子，以等权的形式加入到ICIR加权的基本面复合因子，市值平方，分红因子，日频手工量价因子，高频手工量价因子5因子模型当中，构建7个因子的因子组合。考察以IC和Rank MAE作为Loss函数的深度因子加入后构建组合与基础5因子构建组合在不同的约束条件下的组合表现对比。其组合构建约束如下表：表3不同组合的约束条件全市场多头中证500增强无换手宽约束严约束-周周-1%1%-1%1%-0.30.1-0.3--0.30.3--0.1--0.3--0.3--0.3--0.8-0.30.3资料来源：Wind，国泰海通证券研究所首先考察没有换手约束的全市场多头组合在不考虑交易成本情况下的组合相对中证全指理论超额表现，如下表：表4无换手约束的深度因子全市场多头组合理论超额表现（2017.01-2025.04）年化收益信息比最大回撤29.4%1.67921.3% 市值立方PB高频手工量价-0.0040.0010.010-0.0040.0000.009-0.0